Newsletter: 2. Sunday 11 January 2026Anthroposophy in Hawkes Bay† † † † † † † Kristina Monica Magdalena Friedlander23 July 1955 to 10 January 2026 † † † † † † † Rudolf Steiner Centre, 401 Whitehead Road, Hastings Events in brief over next 2 weeks 11 to 25 January 2026] All is quiet and summery with a scorcher predicted for today.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
**A visitor from Scotland - Christian Maclean - will give a talk at Rangimarie on Friday, 30 January, entitled: “Epiphany: the Adoration of the Magi and the Baptism in the Jordan” Christian has been an Editor for Floris Books for many, many years (and still is!) and for some recent years is a member of the Christian Community Foundation - a group that supports The Christian Community founded in 1922 as a free church, in the area of the donation of the sacraments, teaching, pastoral care and the training and ordination of men and women as priests and of their sending in Europe and overseas. ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ Goetheanum's Foundation StoneAs the double pentagonal dodecahedron, the heart of the Foundation Stone laid under the first Goetheanum and still under the second, is a geometrical form I am offering some musings on GEOMETRY in the intervening weeks, as background. RB Musings on Geometry 2 Let us keep things simple by considering closed, linear, geometrical shapes or forms drawn by straight lines going from point to point and arriving back at the starting point after a number of steps. We can move around a form, say in a clockwise direction. If we start at a point the activity alternates from moving along a line, then turning/rotating at a point, repeating. Distance > angle > distance > angle and so on. A line or lateral, edge or side joins two points or vertices. A joint, knee [-gon {genu}] or ankle [-angle] links two lines at each vertex. I am emphasing the polarity between line [lateral, finite] and point [vertex, infinitesimal].
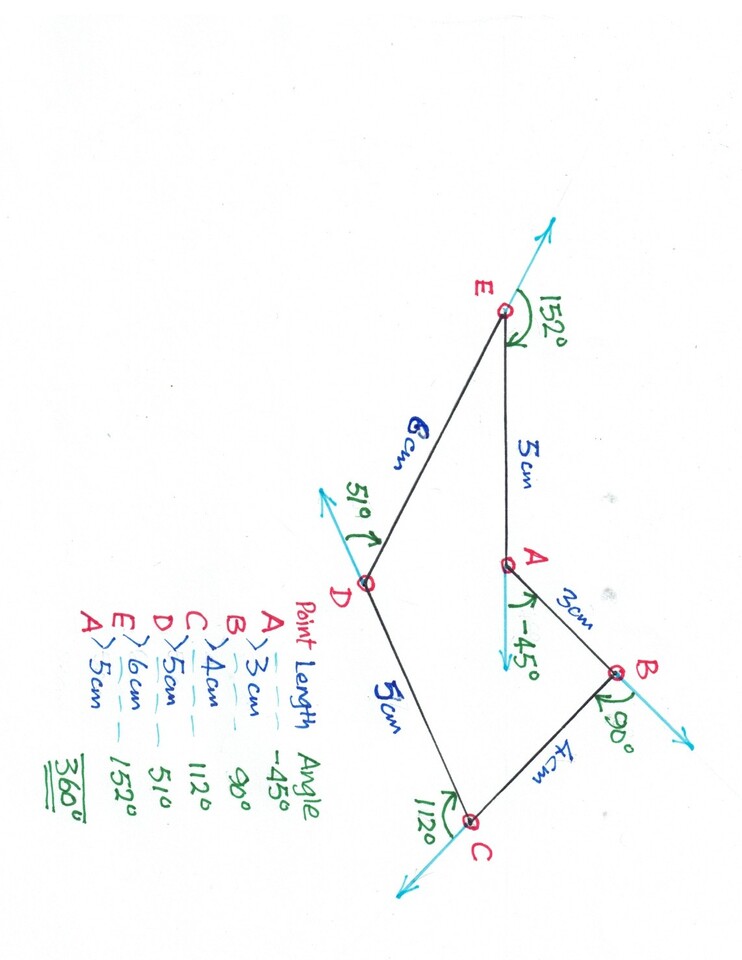
To describe a form, we could count the number of steps, the length of each line between points and the angle of rotation between the lines at each point. In the following diagram of a random, irregular pentagon, a clockwise rotation is measured as positive (+), anticlockwise as negative (-). A complete turn is 360º. The names of these figures are derived from Greek and Latin (see chart of words with numbers in them) so we start with 3 – triangle, 4 – quadrangle, quadrilateral or square, 5 – pentagon, 6 – hexagon, and so on. Let us look at one of the simplest forms: TRIANGLES.
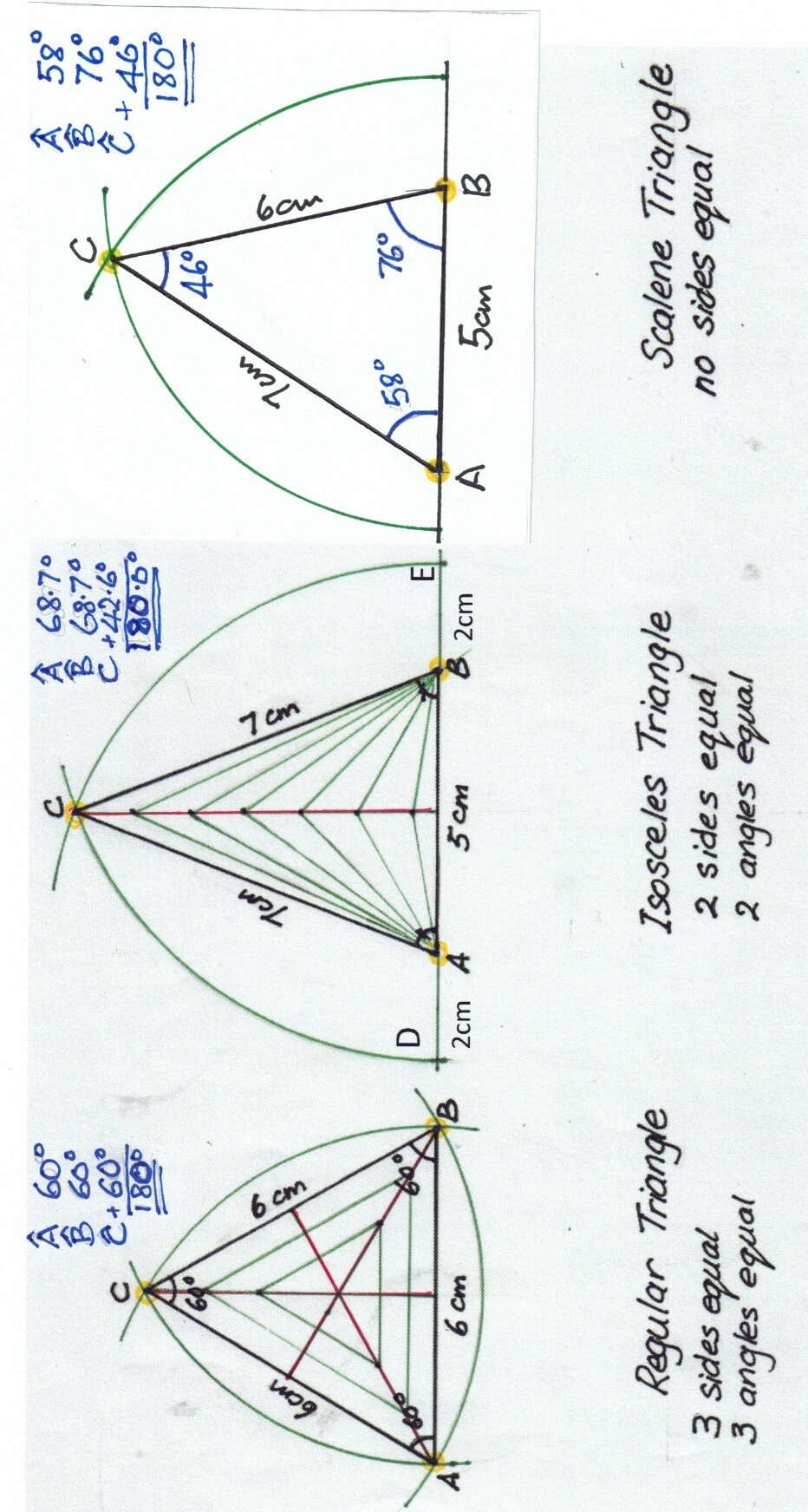
You will also notice that:
Triangles can also be categorised by the size of their largest angle:
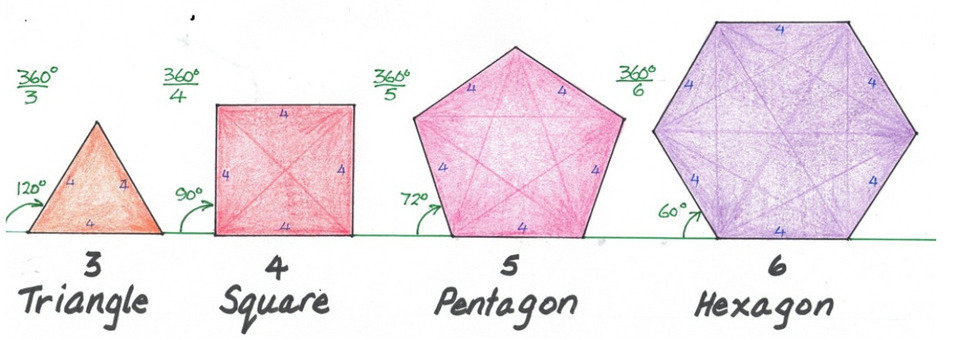
This distinction is very important in the famous Pythagoras Theorem, which we will look at later. The Regular Triangle [tripoint, trilateral, triline, ...] is of special interest because it is unique in its shape, as it is both equiangular and equilateral. Here are the first six Regular Polygons: Triangle [3 sides] to Octagon [8 sides]
Odds and Evens - what do you notice? Next week we will look at the various Centres of a Triangle and the Symmetry of Quadrilaterals. RB
Posted: Thu 08 Jan 2026 |
| © Copyright 2026 Anthroposophy in Hawkes Bay | Site map | Website World - Website Builder NZ |



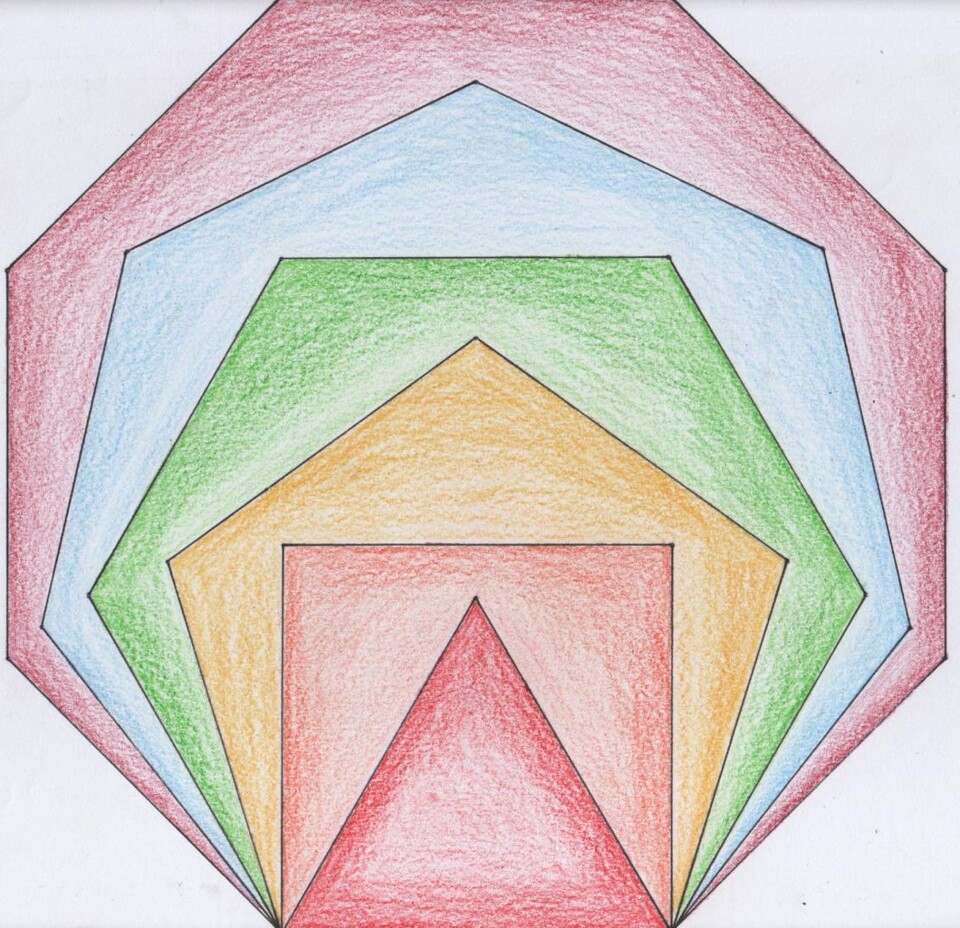
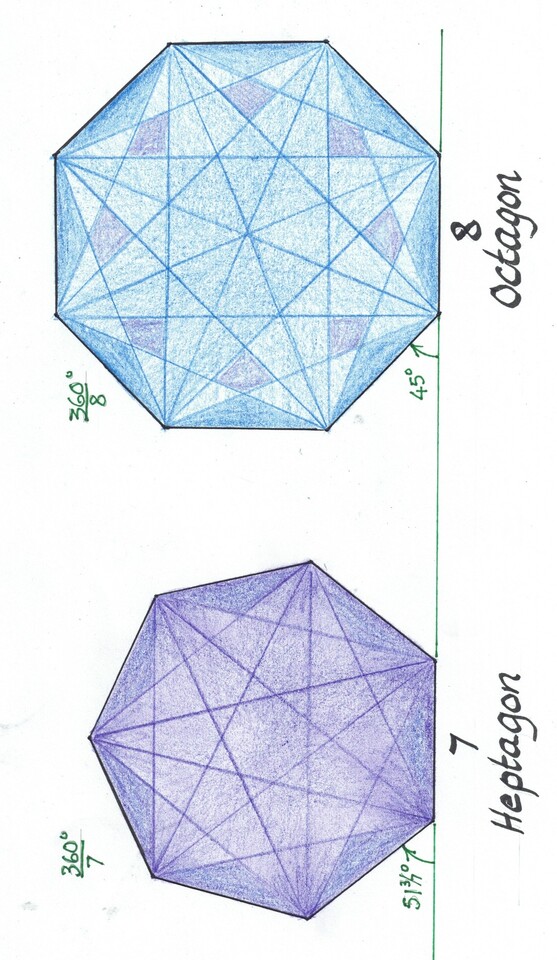 When we nest them all together they look like this:
When we nest them all together they look like this: